Рассмотрим поворотную гомотетию с центром в начале координат, коэффициентом 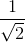   и углом поворота 45°. Если квадрат радиуса R данной окружности – чётное число, то все её целые точки переходят в целые, и мы получаем искомую окружность. Если R² – нечётное число, то все целые точки переходят в центры единичных квадратов с вершинами в целых точках, и искомая окружность получается после переноса на вектор  (½, ½).  Это достаточно очевидно из наглядных соображений – на рисунке изображено действие на целочисленную решетку сначала сжатием, а потом поворотом.

  Более строго. Точка с целыми координатами  (x, y)  под действием указанных поворота и растяжения, переходит в точку с координатами  x'= ½ (x – y), y'= ½ (x + y).  ЕслиR² чётно, тоxиyодной чётности, поэтомуx', y'– целые и  (x')² + (y')² = ½ (x² +y²) = ½R².  Если жеR² нечётно, то чётностьxиyразлична, поэтому после сдвига на вектор  (½, ½)  получим целую точку с координатами  x''= ½ (x – y+ 1), y''= ½ (x + y+ 1)  и (x''– ½)² + (y''– ½)² = ½ (x² + y²) = ½R².

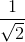
Ответ задачи отсутствует