Задача
Пусть Р – произвольная точка внутри треугольника АВС. Обозначим через А1, В1 и С1 точки пересечения прямых АР, ВР и СР соответственно со сторонами ВС, СА и АВ. Упорядочим площади треугольников АВ1С1, А1ВС1, А1В1С, обозначив меньшую через S1, среднюю – S2, а большую – S3. Докажите, что 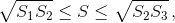 где S – площадь треугольника А1В1С1.
где S – площадь треугольника А1В1С1.
Решение
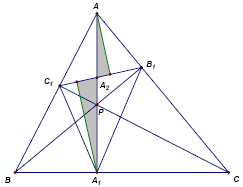
Не ограничивая общности, будем считать, что площади треугольников АВ1С1, А1ВС1, А1В1С соответственно равны S1, S2 и S3. Первый способ. Расположим в вершинах A, B и C такие массы a, b и c, что точка Р – центр тяжести полученной системы материальных точек. Можно считать, что a + b + c = 1. Обозначим через А2 точку пересечения В1С1 и АА1. Поскольку треугольники АВ1С1 и А1В1С1 имеют общее основание, то S1 : S = AA2 : A2A1.
(Это несложно доказать, используя найденные в первом способе отношения площадей.) Рассмотрим функцию Ф(x) = x³ + (S1 + S2 + S3)x² – 4S1S2S3. По теореме Мёбиуса Ф(S) = 0. Кроме того, Ф(x) возрастает на (0, +∞). Поэтому достаточно показать, что 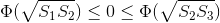 при условии S1 ≤ S2 ≤ S3.
при условии S1 ≤ S2 ≤ S3.
Действительно, 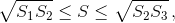 поскольку выражение в скобке очевидно неположительно.
поскольку выражение в скобке очевидно неположительно.
Аналогично 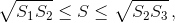
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь