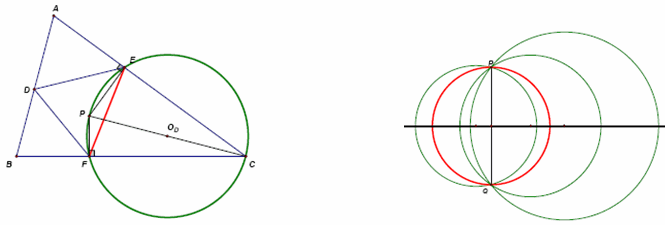
Пусть CР – диаметр описанной окружности треугольника ЕСF. Когда D двигается по АВ с постоянной скоростью, точки E и F, двигаются с постоянными скоростями по прямым АC и ВC. Поэтому и точка P (поскольку  PE ⊥ AC  и  PF ⊥ BC)  двигается с постоянной скоростью, то есть по прямой.

  Следовательно, серединаOотрезкаСР, являющаяся центром указанной окружности, также двигается по прямой. Значит, все эти окружности проходят через точкуQ, симметричнуюСотносительно этой прямой, то есть содержат общую хордуСQ.   Поскольку на хордуEFопирается постоянный уголС, то её длина будет минимальной при минимальном радиусе описанной окружности треугольникаСEF. Cреди всех окружностей, содержащих общую хорду, минимальный радиус будет иметь та из них, для которой эта хордаCQявляется диаметром. Отсюда вытекает следующий способ построения точкиD.   Проведём черезАпрямую, параллельнуюl₂, и найдём точкуUеё пересечения сВС. ЧерезВпроведём прямую, параллельнуюl₁, и найдём точкуVеё пересечения сАС. ПустьQ– вторая точка пересечения описанных окружностей треугольниковACUиBCV, Е– вторая точка пересечения окружности с диаметромCQи прямойАС. Тогда прямая, проходящая черезЕпараллельноl₁, пересекаетАВв искомой точке.

Ответ задачи отсутствует