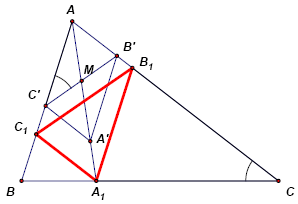
Пусть  AB ≠ AC.  Проведём отрезок B'C' так, чтобы  ∠AC'B' = ∠C.  Ясно, что треугольники АВС и AB′C′ подобны, при этом отрезки B′C′ и ВС не параллельны. Отметим середину М отрезка B′C′ и достроим треугольник до параллелограмма AB′A′C′. Далее найдём точку A₁ пересечения прямых АМ и ВС и построим параллелограмм АВ₁А₁С₁. Отрезки А₁С₁, В₁А₁ и В₁С₁ осуществляют искомое разрезание.

Ответ задачи отсутствует