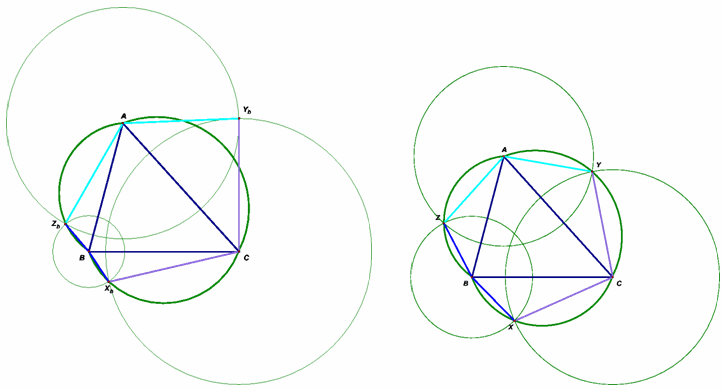
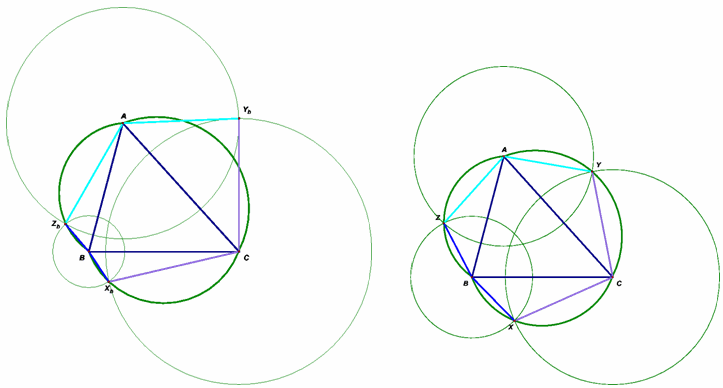
Первый способ. Построим на каждой стороне треугольника во внешнюю сторону дуги, вмещающие угол φ. Покажем, что на дугах BC, CA, AB найдутся такие точки X, Y, Z соответственно, что  AZ = AY,  BZ = BX,  CX = CY.  Пусть AC – наибольшая сторона треугольника, AB – наименьшая. Возьмём произвольную точку Z на дуге AB, найдём на дуге BC такую точку X, что  BX = BZ,  (Х определяется однозначно, так как   AB ≤ BC)  и построим точку Y, лежащую по разные стороны с В от прямой АС и такую, что  AY = AZ,  CY = CX.  При  Z = B  имеем  AY = AB,  CY = CB.  Следовательно,

∠AYC = ∠B < φ  и Y лежит вне сегмента, построенного на АС (рис. слева).

  При  Z = A  точкаYне существует, так как  AC ≥ BC.  Следовательно, при некотором промежуточном положении точкиZ, точкаYпопадает на дугуАС(рис. справа).   Осталось доказать, что из треугольниковABC, ABZ, BCX, ACYможно склеить тетраэдр, то есть что хотя бы в одной из вершинA, B, Cугол треугольникаABCменьше суммы примыкающих к той же вершине углов двух других треугольников (см. задачу187108). Если это не так, то ∠A+ ∠B+ ∠C≥ 3π – 3φ > 3π – 2π = π.  Противоречие.   Второй способ. Для каждого из отрезков AB, BC и CA построим на плоскости множество точек, из которых эти отрезки видны под углом φ – получим шесть дуг. Для BC пусть это множество ω_a, для AC – ω_b и для AB – ω_c. K, L, M  – точки пересечения этих множеств (см. рис.). Рассмотрим пересечение трёх областей с границами из двух дуг (оно непусто, например, ему принадлежит точка Ферма-Торичелли, из которой все стороны треугольника видны под углом ^2φ/₃).   Ясно, чтоMлежит в области, ограниченной ω_a, L– ω_b, аK– ω_c. Множество точек пространства, из которых отрезокBCвиден под углом φ – поверхность, получающаяся при вращении ω_aотносительноBC. Обозначим еёF_a. Аналогично получим ещё две поверхности –F_b, F_c. ПересечениемF_aиF_bбудет некоторая непрерывная кривая, проходящая черезCиK, причёмKлежит внутри тела, ограниченногоF_c, аC– вне его. Значит, линия пересеченияF_aиF_bбудет также пересекать иF_c.

Ответ задачи отсутствует