Задача
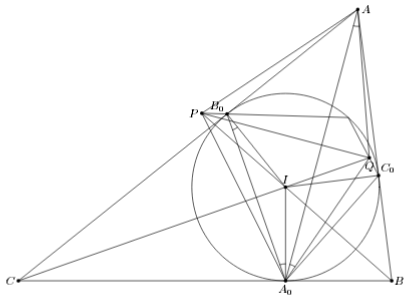
Вписанная окружность ω треугольника ABC касается сторон BC, AC и AB в точках A0, B0 и C0 соответственно. Биссектрисы углов B и C пересекают серединный перпендикуляр к отрезку AA0 в точках Q и P соответственно. Докажите, что прямые PC0 и QB0 пересекаются на окружности ω.
Решение
Из определения точек P, Q следует, что они лежат на описанных окружностях треугольников ABA0 и ACA0 соответственно. Поэтому треугольник AA0Q подобен треугольнику B0A0I, а треугольник AA0P – треугольнику C0A0I (по двум углам). Значит, A0Q·A0B0 = A0I·A0A = A0P·A0C0. Кроме того,
∠PA0Q = ½ (∠B + ∠C) = ∠B0A0C0, поэтому треугольники A0PQ и A0B0C0 подобны (см. рис.). Следовательно, треугольники A0B0P и A0C0Q тоже подобны (по углу и двум сторонам), то есть угол между прямыми B0P и C0Q равен углу B0A0C0, что и требовалось.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь