Решение 1:   Так как точки A, C, H_A, H_C лежат на одной окружности, достаточно доказать, что прямые AC, H_AH_C и TL пересекаются в одной точке. Проецируя вершины гармонического четырёхугольника ABCL из точки T на прямую AC, получаем, что точка пересечения TL с AC образует гармоническую четвёрку с точками A, C, H_B. По теореме Менелая прямая H_AH_C пересекает AC в этой же точке.

Решение 2:   Пусть M – середина AC. Обозначим описанные окружности треугольников AHC, BH_AH_C и четырёхугольника AH_CH_AC соответственно ω₁, ω₂, ω₃. Как известно, окружности ω₁ и ω симметричны относительно прямой AC (см. задачу 155463). Пусть окружности ω₂ и ω повторно пересекаются в точке P, а ω₂ и ω₁ – в точке N.

  Известно, что точки M, H и P лежат на одной прямой (см. задачу 166146), а  ∠BPH = 90°.

  Пусть прямые BP и AC пересекаются в точке S. Тогда H – ортоцентр треугольника BMS. Следовательно,  SH ⊥ BM,  то есть точка N лежит на медиане BM.

  Поскольку дуги CN, AD и CL равны, то точки N и L симметричны относительно AC.

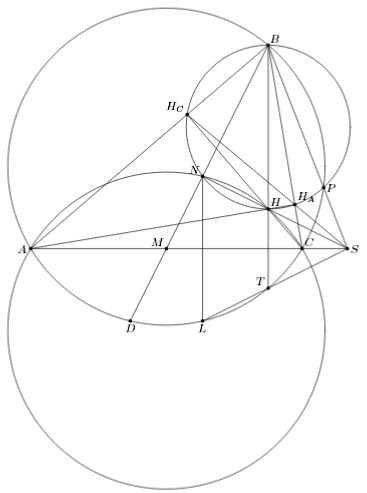
  Заметим, что S – радикальный центр как окружностей ω, ω₁, ω₂, так и окружностей ω, ω₂, ω₃, поэтому радикальная ось NH окружностей ω₁ и ω₂, а также радикальная ось H_CH_A окружностей ω₂ и ω₃ проходят через S. Прямые NH и LT симметричны относительно AC, поэтому они пересекаются в точке S (см. рис.). Степени точки S относительно ω и ω₂ равны, то есть  SH_A·SH_C = ST·SL.  Следовательно, точки H_A, H_C, T, L лежат на одной окружности.

Ответ задачи отсутствует