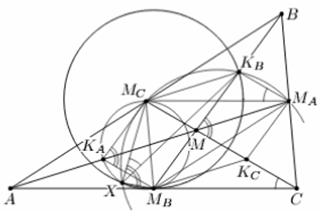
Пусть K_A, K_B и K_C – середины отрезков AM, BM и CM соответственно (см. рис.). Тогда  M_CK_B || AM  и  K_BM_A || MC,  как средние линии треугольников ABM и CBM соответственно; значит,  ∠M_CK_BM_A = ∠AMC.  Аналогично  ∠M_CK_AM_B = ∠BMC  и  ∠M_AK_CM_B = ∠BMA; следовательно,  ∠M_CK_AM_B + ∠M_BK_CM_A + ∠M_AK_BM_C = 360°.

  Согласно задаче156622описанные окружности треугольниковM_CK_AM_B, M_BK_CM_AиM_AK_BM_Cимеют общую точкуX. При этом ∠(K_BX, XM_B) = ∠(K_BX, XM_C) + ∠(M_CX, XM_B) = ∠(K_BM_A, M_AM_C) + ∠(M_CK_A, K_AM_B) = ∠(MC, CA) + ∠(BM, MC) = ∠(BM, CA) = ∠(K_BM_B, AC).   Это равенство означает, что окружность Ω_Bпроходит через точкуX.   Аналогично черезXпроходят окружности Ω_Aи Ω_C.

Ответ задачи отсутствует