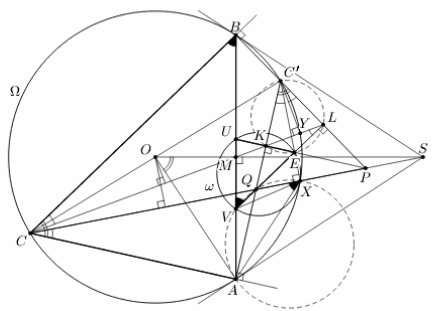
Пусть данные перпендикуляры, проходящие через K и L, пересекают AB в точках U и V соответственно и пересекаются в точке E. Заметим, что обе прямые AC и KE перпендикулярны прямой AC', так что  AC || KE;  аналогично  BC || LE.  Пусть прямая C'E вторично пересекает окружность Ω в точке X (см. рис.). Мы докажем, что X – точка касания окружностей ω и Ω.   Первый способ. Точки K и L лежат на окружности с диаметром C'E. Поэтому  ∠ACX = ∠AC'X = ∠KLE = ∠LCB = ∠MCB.  Это значит, что прямая CX – симедиана треугольника ABC; как известно (см. задачу 156983), она проходит через точку S пересечения касательных к Ω в точках A и B.

  ПустьO– центр Ω,  ∠C= γ,  аCMвторично пересекает Ω в точкеY. Так какAM– высота прямоугольного треугольникаOAS, то  OM·OS = OA² =OC²;  это значит, что треугольникиOMCиOCSподобны. Значит, отношение их высот, опущенных изO, равно  ^OM/_OC = ^OM/_OA= cos γ.  Эти высоты являются средними линиями прямоугольных треугольниковCYC'иCXC', так что  ^C'Y/_C'X= cos γ.   Пусть прямыеAC'иBC'пересекаютCXв точкахQиPсоответственно. Заметим, что  ∠PC'Q= ∠YCB= γ.  Кроме того, ∠YC'L= ∠YCB= ∠QC'X,  так что прямоугольные треугольникиYC'LиXC'Qподобны. Значит,  ^C'L/_C'Q = ^C'Y/_C'X= cos γ = cos∠PC'Q.  Отсюда следует, чтоQL– высота треугольникаPC'Q. Итак, точкиL, E, QиVлежат на одной прямой.   Поскольку  ∠QVB= ∠VBC= ∠AXC,  четырёхугольникAVQXвписан в некоторую окружность. Заметим, что точкиXиKлежат на окружности с диаметромEQ. Из этих двух окружностей получаем  ∠UEX= ∠KEX= ∠AQX= ∠AVX,  то есть точкаXтакже лежит на ω. Кроме того, ∠EVX= ∠QAX= ∠C'AX.  Это означает, что градусные меры дугC'XиEXокружностей Ω и ω равны. Значит, касательные к этим окружностям, проведённые в точкеX, совпадают, то есть окружности Ω и ω касаются в точкеX.   Второй способ. Обозначим через A₁, B₁ и C₁ точки пересечения прямой C'E с прямыми BC, CA и AB соответственно. Как и выше, равенство

∠ACX = ∠AC'X = ∠KLE = ∠LCB  означает, что  ∠ACX = ∠KCB;  с другой стороны, из равенства  ∠KC'L = ∠KC'E = ∠KCA₁  следует также, что точки C, C', K и A₁ лежат на одной окружности (см. рис.). Отсюда  ∠C'KA₁ = ∠C'CB = ∠C'AB,  то есть  KA₁ || AB.

  Обозначим черезNточку пересечения прямыхKA₁иAC. Поскольку  AB || A₁K  и прямаяCMделитABпополам, она делит пополам иA₁N, то есть KN = KA₁.  Так как  KE || AB₁, KE– средняя линия треугольникаA₁NB₁, то есть  B₁E = EA₁.   ПустьX'– точка Ω, диаметрально противоположнаяX, а прямыеX'AиX'Bпересекают прямуюC'Eв точкахSиTсоответственно. Тогда  ∠SX'T= ∠C  и  ∠X'ST= 90° – ∠SX'C'= 90° – ∠;ABC'= ∠B,  то есть треугольникиABCиTSX'подобны. Более того, поскольку  ∠SX'X= ∠ACX= ∠BCM,  точкиMиXв этих треугольниках соответственны, то есть  SX = XT.   Из равенства  ∠AST= ∠B= ∠C₁BA₁  следует, что точкиS, A, BиA₁лежат на одной окружности, откуда  C₁A·C₁B = C₁S·C₁A₁.  Аналогично C₁A·C₁B = C₁T·C₁B₁,  поэтому  C₁S·C₁A₁=C₁T·C₁B₁,  или  ^C₁S/_C1B1=^C₁T/_C1A1.  Это значит, что отрезкиA₁B₁иTSгомотетичны с центром вC₁; эта гомотетия переводит серединуEотрезкаA₁B₁в серединуXотрезкаST. Следовательно,  ^C₁S/_C1B1=^C₁X/_C1E,  или  ^C₁S/_C1X=^C₁B₁/_C1E.  В силу параллельности  AB₁иUE ^C₁A/_C1U=^C₁B₁/_C1E=^C₁S/_C1X,  поэтому  UX || AS.  Отсюда  ∠UXE= ∠ASX= ∠B= ∠EVU,  то есть точкаXлежит на ω.   Наконец, рассмотрим треугольникиABCиUVE;их соответственные стороны параллельны, так что они гомотетичны (с отрицательным коэффициентом). При этой гомотетии прямаяCX'переходит вEX(поскольку  C'X || CX'),  окружность Ω переходит в окружность ω, a значит,X'переходит вX. Поэтому касательная к ω в точкеXпараллельна касательной к Ω в точкеX', а значит – и касательной к Ω в точкеX. Отсюда следует, что ω и Ω касаются в точкеX.

Ответ задачи отсутствует