Задача
Васе задали на дом уравнение x² + p1x + q1 = 0, где p1 и q1 – целые числа. Он нашел его корни p2 и q2 и написал новое уравнение x² + p2x + q2 = 0. Повторив операцию еще трижды, Вася заметил, что он решал четыре квадратных уравнения и каждое имело два различных целых корня (если из двух возможных уравнений два различных корня имело ровно одно, то Вася всегда выбирал его, а если оба – любое). Однако, как ни старался Вася, у него не получилось составить пятое уравнение так, чтобы оно имело два различных вещественных корня, и Вася сильно расстроился. Какое уравнение Васе задали на дом?
Решение
Пятое уравнение с целыми коэффициентами не должно иметь различных вещественных корней. Значит, если его коэффициенты обозначить через p5 и q5, то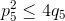 
и 
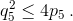Оба числа положительны, и при этом, возводя в квадрат первое неравенство и подставляя условие из второго, получаем 
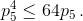Отсюда
оба числа меньше 5, и перебором находим единственную подходящую пару: 1 и 2.
Найденные коэффициенты пятого уравнения являются корнями четвёртого; по теореме Виета находим само четвёртое уравнение: x² – 3x + 2 = 0. Продолжая применять теорему Виета, последовательно находим третье, второе и, наконец, первое уравнения: x² + x – 6 = 0, x² + 5x – 6 = 0,
x² + x – 30 = 0.
Ответ
x² + x – 30 = 0.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь