Решение 1:   Для начала покажем, что ответ единственен. Рассмотрим два равносторонних пятиугольника ABCDE и A'B'C'D'E', в которых  ∠A = ∠A' = 120°,

∠C = ∠C' = 135°.  Можно считать, что длины сторон пятиугольников равны 1. Заметим, что по двум сторонам и углу между ними равны треугольники EAB и E'A'B', а также BCD и B'C'D'. Значит,  BE = B'E',  BD = B'D',  и треугольники BDE и B'D'E' равны по трём сторонам. Следовательно,

∠BDE = ∠B'D'E'.  Из равнобедренных треугольников BCD и B'C'D' видно, что  ∠CDB = ∠C'D'B' = 22,5°.  Таким образом,

∠CDE = ∠CDB + ∠BDE = ∠C'D'B' + ∠B'D'E' = ∠C'D'E',  что и означает единственность ответа.

  Докажем, что существует удовлетворяющий условию пятиугольник, у которого  ∠D = 90°.  Сначала построим прямоугольный треугольник CDE, с катетами CD и DE, равными 1. Тогда 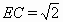 .  Затем построим такую точку B, что  ∠ECB = 90°,  BC = 1.  Тогда  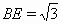.  Теперь построим точку A так, что  ∠AEB = ∠ABE = 30&deg. Тогда  ∠BAE = 120°,  AB = AE = 1.

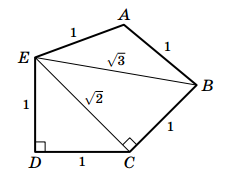
Решение 2:   Пусть длины всех сторон пятиугольника равны 1. Из треугольника BDC находим, что  ∠BDC = 12,5°.  Обозначим  ∠BDE = φ.  По теореме косинусов 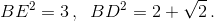   По той же теореме  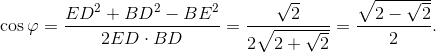   Значит,  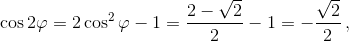   то есть  2φ = 135°,  φ = 72,5°,  а  ∠D = ∠EDB + ∠BDC = 90°.

90°.