Задача
Каждая боковая грань пирамиды является прямоугольным треугольником, в котором прямой угол примыкает к основанию пирамиды. В пирамиде проведена высота. Может ли она лежать внутри пирамиды?
Решение
Пусть основанием пирамиды SA1...An является многоугольник A1...An (см. рисунки). Возможны два случая.
1) Соседние углы в двух соседних боковых гранях – прямые. Пусть, например, ∠SA2A1 = ∠SA2A3 = 90° (рис. слева). Тогда по признаку перпендикулярности прямой и плоскости SA2 ⊥ A1A2A3, то есть SA2 – высота пирамиды, и она принадлежит боковой поверхности пирамиды.
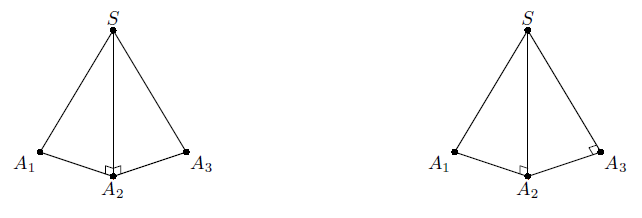
Ответ
Не может.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет