Задача
Через точку P проведены три отрезка, параллельные сторонам треугольника ABC (см. рисунок).
Докажите, что площади треугольников A1B1C1 и A2B2C2 равны.
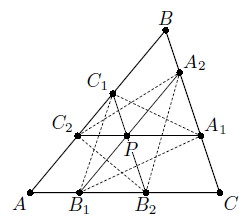
Решение
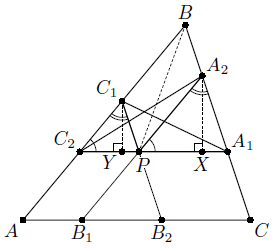
Заметим, что SA2B2C2 = SA2C2P + SB2C2P + SA2B2P, а SA1B1C1 = SA1C1P + SB1C1P + SA1B1P. Докажем, что SA2C2P = SA1C1P (для других пар площадей равенство доказывается аналогично). Это можно доказать различными способами. Первый способ. Поскольку C2PA2B – трапеция, то SA2C2P = SBA2P. Так как BC1PA2 – параллелограмм, то SBA2P = SBC1P. И, наконец, из того, что BC1PA1 – трапеция, получим, что SBC1P = SA1C1P . Следовательно, SA2C2P = SA1C1P.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет