Пусть F – точка пересечения прямых KO и XL (см. рис.). Докажем, что ∠KFX = 90°.

 Первый способ. Обозначим  ∠KNL= α.  Тогда центральный угол  ∠MOK= 2α,  а  ∠XKO= –MKO= 90° – α.  ТреугольникиXKLиNKLравны (по двум сторонам и углу между ними). Следовательно,  ∠KXL= ∠KNL= α   (*).   Тогда в треугольникеXKF ∠KFX= 180° – (90° – α) – α = 90°.   Второй способ. Проведём высоту KH треугольника MKN.  ∠MKO = ∠NKH  (см. задачу 152358). При симметрии относительно прямой KL точка N переходит в точку X, прямая LN переходит в прямую LX, прямая KH переходит в прямую KO.

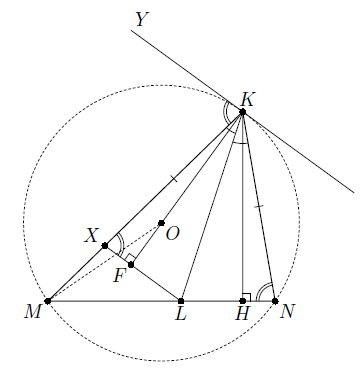
  Поскольку  KH ⊥ LN,  то и образы этих прямых при симметрии также перпендикулярны, следовательно,  KO ⊥ XL.   Третий способ. Пусть KY – касательная к описанной окружности треугольника MKN. Используя угол между касательной и хордой и утверждение (*), получим, что  ∠YKX = ∠KNL = ∠KXL.  Значит, прямая XL параллельна KY, то есть перпендикулярна KO.

Ответ задачи отсутствует