Задача
Известно, что среди членов некоторой арифметической прогрессии a1, a2, a3, a4, ... есть числа 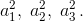
Докажите,что эта прогрессия состоит из целых чисел.
Решение
a3 – a2 = a2 – a1 = d – разность прогрессии. 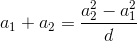 и
и 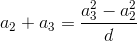 – целые числа, значит, a3 – a1 = 2d целое, а d целое или полуцелое. Поскольку 2a1 + d = a1 + a2 – целое число, возможны три случая: a1 и d (а значит, и все члены прогрессии) целые; d целое, a1 полуцелое; d полуцелое, a1 – дробь со знаменателем 4. Но в последних двух случаях ясно, что знаменатель каждого члена тот же, что у a1. С другой стороны, знаменатель
– целые числа, значит, a3 – a1 = 2d целое, а d целое или полуцелое. Поскольку 2a1 + d = a1 + a2 – целое число, возможны три случая: a1 и d (а значит, и все члены прогрессии) целые; d целое, a1 полуцелое; d полуцелое, a1 – дробь со знаменателем 4. Но в последних двух случаях ясно, что знаменатель каждого члена тот же, что у a1. С другой стороны, знаменатель 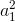 больше знаменателя a1. Противоречие.
больше знаменателя a1. Противоречие.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет