Задача
Пусть C – одна из точек пересечения окружностей α и β. Касательная в этой точке к α пересекает β в точке B, а касательная в C к β пересекает α в точке A, причём A и B отличны от C, и угол ACB тупой. Прямая AB вторично пересекает α и β в точках N и M соответственно. Докажите, что 2MN < AB.
Решение
По теореме об угле между касательной и хордой ∠ACM = ∠CBA и ∠BCN = ∠CAB. Поскольку угол ACB тупой, точки A, M, N, B лежат на прямой AB именно в таком порядке. По теореме о касательной и секущей AM = AC²/AB и BN = BC²/AB. Применив сначала неравенство Коши, а затем неравенство треугольника, получаем, что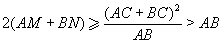 
,
что равносильно доказываемому неравенству.
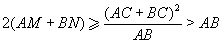
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет