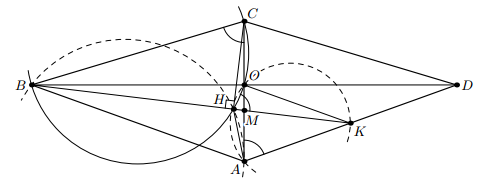
Достроим треугольник до ромба ABCD. Пусть O – центр ромба. Тогда прямая BM делит медиану AO треугольника ABD в отношении  2 : 1.  Значит, эта прямая тоже является медианой, то есть проходит через середину K отрезка AD.

  Заметим, что точки O и H лежат на окружности с диаметром BC. Далее можно рассуждать по-разному.   Первый способ.  ∠KHO = ∠BCO = ∠KAO.  Следовательно, четырёхугольник AHOK – вписанный и  ∠AHK = ∠AOK = 80°,  а  ∠AHB = 100°  (см. рис.).

100°.