Задача
Длина гипотенузы прямоугольного треугольника равна 3.
а) Рассеянный Учёный вычислил дисперсию длин сторон этого треугольника и нашёл, что она равняется 2. Не ошибся ли он в расчетах?
б) Какое наименьшее стандартное отклонение сторон может иметь такой прямоугольный треугольник? Какие у него при этом катеты?
Решение
а) Пусть a и b – катеты треугольника. Тогда a² + b² = 9, а D = ⅓ (a² + b² + 9) – &frac19; (a + b + 3)² = 18/3 – 1/9 (a + b + 3)² = 6 – 1/9 (a + b + 3)². Из неравенства треугольника следует, что a + b > 3. Значит, D < 6 – 1/9·6² = 2. б) Из неравенства между средним арифметическим и средним квадратичным следует, что 
. Значит, 
Следовательно, стандартное отклонение 
длин трёх сторон не превосходит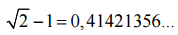 
Это наименьшее значение достигается, только если дисперсия катетов равна нулю, то есть если 
.
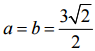Ответ
а) Ошибся; б)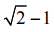 
; .
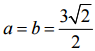Чтобы оставлять комментарии, войдите или зарегистрируйтесь