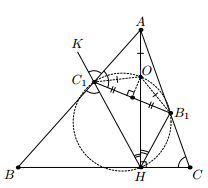
Решение 1:   Пусть O – центр описанной окружности треугольника AB₁C₁ (см. рис.). Четырёхугольник BC₁B₁B – вписанный, следовательно, B₁C₁ и BC антипараллельны. Значит, треугольник AB₁C₁ гомотетичен треугольнику с вершинами в точке A и основаниях высот, опущенных из вершин B и C. Поэтому из задачи 152358 следует, что точка O лежит на высоте AH. Кроме того, O принадлежит серединному перпендикуляру к отрезку B₁C₁.

  Рассмотрим треугольникHB₁C₁. БиссектрисаHAи серединный перпендикуляр к сторонеB₁C₁не совпадают, поэтому пересекаются в серединеOдугиB₁C₁его описанной окружности. С другой стороны, посколькуO– центр описанной окружности треугольникаAB₁C₁, то  OA = OB₁=OC₁.  Следовательно,A– центр вневписанной окружности треугольникаHB₁C₁(это следует излеммы о трезубце, см. задачи153119и152395). Поэтому ∠BC₁H= ∠KC₁A= ∠AC₁B₁= ∠ACB.  Таким образом, четырёхугольникAC₁HC– вписанный, откуда  ∠CC₁A= ∠CHA= 90°. Аналогично ∠BB₁A= 90°.

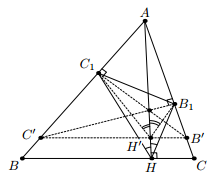
Решение 2:   Воспользуемся тем, что высоты треугольника содержат биссектрисы углов его ортотреугольника (см. задачу 152866). Заметим также, что если одна из точек B₁ или C₁ является основанием высоты, то и другая тоже. Пусть B₁ и C₁ – не основания высот.   Первый способ. Восстановим из этих точек перпендикуляры до пересечения с прямыми AC и AB в точках B' и C' соответственно (рис. слева). Тогда C'B₁ и B'C₁ – высоты треугольника AB'C', следовательно, B₁C₁ и B'C' антипараллельны. Значит,  BC || B'C',  то есть AH' – высота треугольника AB'C' (H' – точка пересечения AH и B'C'). Поэтому ∠C₁H'A = ∠B₁H'A.  По условию  ∠C₁HA = ∠B₁HA,  следовательно, треугольники C₁HH' и B₁HH' равны, откуда  HB₁ = HC₁.  Тогда  HA ⊥ B₁C₁,  следовательно,  B₁C₁ || BC,  то есть треугольник ABC – равнобедренный. Противоречие.

  Второй способ. Проведём высоты BH_b и CH_c (рис. справа), а также перпендикуляры AK, AL, H_cN и H_bM к прямым HC₁ и HB₁. Поскольку

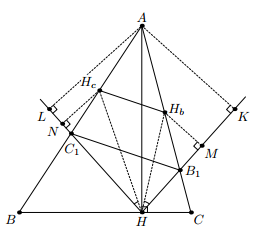
B₁C₁ || H_bH_c,  то  H_cN : AL = H_cC₁ : AC₁ = H_bM : AK.  Поскольку HA – биссектриса угла C₁HB₁, то  AK = AL,  поэтому  H_cN = H_bM.  Так как HA также биссектриса угла H_cHH_b, то  ∠H_cHN = ∠H_bHM,  следовательно, треугольники HH_cN и HH_bM равны. Таким образом, ортотреугольник треугольника ABC – равнобедренный, поэтому ABC – тоже равнобедренный. Противоречие.

Ответ задачи отсутствует