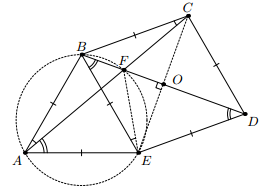
Задача
На стороне BE правильного треугольника ABE вне его построен ромб BCDE. Отрезки AC и BD пересекаются в точке F. Докажите, что AF < BD.
Решение
Треугольник ABC – равнобедренный, следовательно, ∠BAC = ∠BCA (см. рис.). Кроме того, в силу симметрии, ∠BCA = ∠BEF. Следовательно, ∠BAF = ∠BEF, то есть четырёхугольник ABFE – вписанный. Значит, ∠AFE = ∠ABE = 60° и ∠DFE = ∠BAE = 60°. Кроме того,
∠FDE = ∠FBE = ∠FAE, поэтому ∠AEF = ∠DEF. Следовательно, треугольник AEF равен треугольнику DEF по двум сторонам и углу между ними. Таким образом, AF = DF < BD, что и требовалось.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет