Рассмотрим поворотную гомотетию F с центром в начале координат, коэффициентом 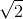   и углом 45°. Заметим, что в координатах её можно записать как  F: (x, y) → (x – y, x + y),  то есть образ целочисленной решетки снова лежит в целочисленной решётке. При этом площадь каждой фигуры увеличивается вдвое, так что образ треугольника X имеет площадь 2S.

  Заметим, что образ единичного квадрата, независимо от его цвета, имеет равные чёрную и белую часть площади, то есть для него утверждение задачи верно. Следовательно, оно верно для любого прямоугольника с вершинами в узлах решётки и сторонами, параллельными осям координат.

  Если стороны такого прямоугольника имеют одинаковую чётность, то образ вектора его диагонали имеет чётные координаты, и тогда центр образа прямоугольника – узел решётки.

  Если же стороны прямоугольника имеют разную чётность, то образ вектора его диагонали имеет нечётные координаты, и тогда центр образа прямоугольника совпадает с центром одного из квадратов решётки.

  В любом случае при центральной симметрии относительно такой точки чёрная клетка переходит в чёрную, а белая – в белую. Следовательно, образ всякого прямоугольного треугольника в вершинами в узлах решётки и катетами, параллельными осям координат, имеет равные чёрную и белую площадь. Ну а любой треугольник можно получить, вырезав из прямоугольника несколько таких треугольников.

Ответ задачи отсутствует