Задача
При всяком ли натуральном n > 2009 из дробей 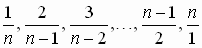 можно выбрать две пары дробей с одинаковыми суммами?
можно выбрать две пары дробей с одинаковыми суммами?
Решение
Каждая из данных дробей имеет вид 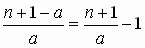 , где 1 ≤ a ≤ n. Стало быть, достаточно найти такие различные натуральные числа a, b, c и d, не большие 2009, для которых
, где 1 ≤ a ≤ n. Стало быть, достаточно найти такие различные натуральные числа a, b, c и d, не большие 2009, для которых 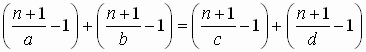 . Убрав минус единицы и поделив затем на n + 1, получим равносильное равенство
. Убрав минус единицы и поделив затем на n + 1, получим равносильное равенство 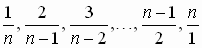 . Осталось подобрать удовлетворяющие ему дроби. Это можно сделать, взяв любое равенство двух сумм различных натуральных слагаемых, НОК которых не больше 2009, и поделив его на этот НОК. Например, поделив равенство 1 + 4 = 2 + 3 на 12, получим
. Осталось подобрать удовлетворяющие ему дроби. Это можно сделать, взяв любое равенство двух сумм различных натуральных слагаемых, НОК которых не больше 2009, и поделив его на этот НОК. Например, поделив равенство 1 + 4 = 2 + 3 на 12, получим  .
.
Ответ
При всяком.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет