Задача
Дан треугольник ABC и прямая l. Прямые, симметричные l относительно AB и AC пересекаются в точке A1. Точки B1, C1 определяются аналогично. Докажите, что
а) прямые AA1, BB1, CC1 пересекаются в одной точке;
б) эта точка лежит на описанной окружности треугольника ABC ;
в) точки, построенные указанным способом для двух перпендикулярных прямых, диаметрально противоположны.
Решение
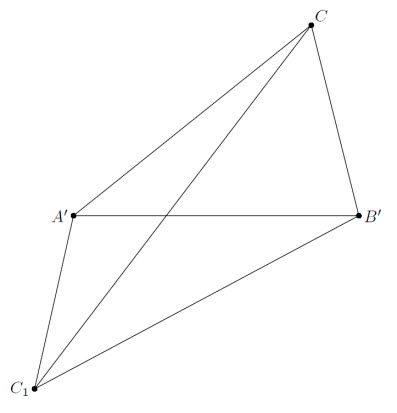
Заметим, что, когда прямая l движется параллельно себе с постоянной скоростью, прямые, симметричные l относительно AC и BC, также перемещаются параллельно себе с постоянной скоростью. Поэтому точка C1 движется по прямой, проходящей через C, то есть точка пересечения CC1 с описанной окружностью зависит только от направления прямой l. Пусть теперь A', B' – точки пересечения l с BC и AC (см. рис.). Тогда B'C – биссектриса одного из углов между прямыми B'C1 и B'A', а A'C – биссектриса одного из углов между прямыми A'C1 и A'B'. Значит, C – центр вписанной или вневписанной окружности треугольника A'B'C1, то есть C1C – биссектриса угла A'C1B' или смежного с ним. Но угол между прямыми A'C1 и B'C1 не зависит от l, значит, не зависит от l и угол между CC1 и C1A'. Поэтому при вращении l с постоянной скоростью прямые AA1, BB1, CC1 вращаются с той же скоростью, откуда следуют все три утверждения задачи.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь