Задача
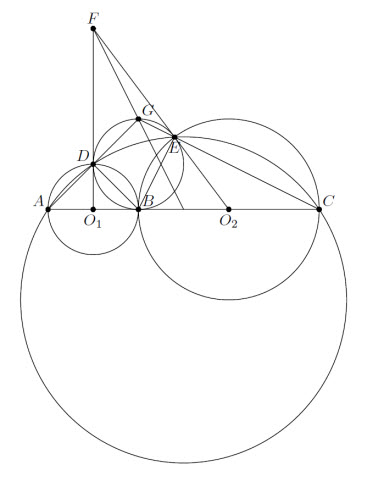
На хорде AC окружности ω выбрали точку B. На отрезках AB и BC как на диаметрах построили окружности ω1 и ω2 с центрами O1 и O2, которые пересекают ω второй раз в точках D и E соответственно. Лучи O1D и O2E пересекаются в точке F. Лучи AD и CE пересекаются в точке G.
Докажите, что прямая FG проходит через середину AC.
Решение
Так как углы ADB и BEC прямые, точки D и E лежат на окружности Ω с диаметром BG. При этом ∠FDG = ∠ADO1 = ∠DAC = ∠GED. Следовательно, FD – касательная к Ω (см. рис.). То же верно для прямой FE. Значит, прямая FG – симедиана треугольника GED (см. задачу 156983). Поскольку треугольник GDE подобен треугольнику GCA, в треугольнике GCA прямая FG будет медианой.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь