Задача
В остроугольном треугольнике ABC AA1, BB1 и CC1 – высоты. Прямые AA1 и B1C1 пересекаются в точке K. Окружности, описанные вокруг треугольников A1KC1 и A1KB1, вторично пересекают прямые AB и AC в точках N и L соответственно. Докажите, что
а) сумма диаметров этих окружностей равна стороне BC. б)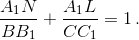 
Решение
а) Треугольники AB1C1, A1BC1 и A1B1C подобны треугольнику ABC с коэффициентами cos A, cos B, cos C соответственно. Поэтому
∠KA1C1 = ∠KA1B1 = 90° – ∠A, и по теореме синусов диаметры описанных окружностей треугольников AKB1 и A1KC1 равны соответственно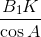 
и 
Следовательно, их сумма равна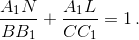 
б) Доказанное в предыдущем пункте равенство можно переписать в виде 
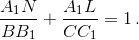Разделив его на BC, получим искомое соотношение.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь