Задача
Докажите, что для любого неравнобедренного треугольника
, где l1, l2 – наибольшая и наименьшая биссектрисы треугольника, S – его площадь.
Решение
Пусть a > b > c – стороны треугольника, 2α, 2β, 2γ – соответствующие им углы. Пусть l – биссектриса наибольшего угла, тогда
S = ½ bc sin 2α = ½ (b + c)l sin α. Отсюда и из аналогичных соотношений для других биссектрис видно, что l – наименьшая биссектриса, то есть
l = l2. Поэтому правое неравенство можно переписать в виде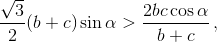 
или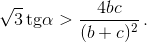 
Но π/6 < α < π/2, следовательно, левая часть больше 1, а правая меньше 1 по неравенству Коши.
Так как 2γ < π/3, то
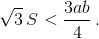С другой стороны, 
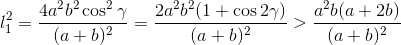(поскольку b > c, то
b cos 2γ > a/2). Поэтому левое неравенство следует из того, что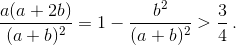 
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь