Задача
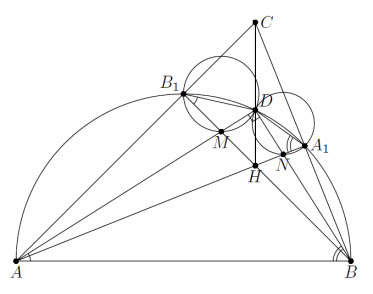
Высоты AA1 и BB1 треугольника ABC пересекаются в точке H. Прямая CH пересекает полуокружность с диаметром AB, проходящую через точки A1 и B1, в точке D. Отрезки AD и BB1 пересекаются в точке M, BD и AA1 – в точке N. Докажите, что описанные окружности треугольников B1DM и A1DN касаются.
Решение
Угол между касательной к описанной окружности треугольника B1DM в точке D и прямой AD равен ∠MB1D = ∠BB1D = ∠BAD (см. рис.). Аналогично угол между касательной к описанной окружности треугольника A1DN и BD равен углу ABD. Поскольку ∠BAD + ∠ABD = 90° = ∠ADB, касательные к обеим окружностям совпадают.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет