Задачи и олимпиады по математике

Задача

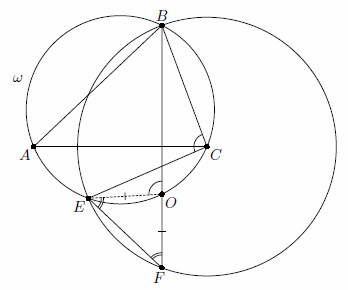
Дан остроугольный треугольник ABC. Окружности с центрами A и C проходят через точку B, вторично пересекаются в точке F и пересекают описанную окружность ω треугольника ABC в точках D и E. Отрезок BF пересекает окружность ω в точке O. Докажите, что O – центр описанной окружности треугольника DEF.

Решение

Пусть в окружности с центром C центральный угол BCE равен 2α. Тогда вписанный угол EFB равен α (см. рис.).

Вписанные в окружность ω углыBCEиBOE, то есть ∠BOE= ∠BCE= 2α. УголBOE– внешний угол треугольникаEOF. Следовательно, ∠OEF= ∠BOE– ∠OFE= α, то есть треугольникEOF– равнобедренный и OE = OF. Аналогично OF = OD. Следовательно,O– центр описанной окружности треугольникаDEF.

Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления