Предположим, что такой тетраэдр существует. Тогда его грани DАВ и DAC – равнобедренные треугольники с вершиной А. Пусть

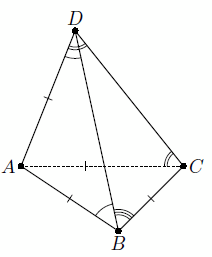
∠ADB = ∠ABD = α,  ∠DBC = β,  ∠DCB = γ,  ∠ADC = ∠ACD = δ,  тогда  ∠BDC = 180° – β – γ (см. рис.).

  Так как треугольникАВС– равносторонний, то  α + β = γ + δ = 90°,  значит,  α + β + γ + δ = 180°.  Тогда   ∠BDC= 180° – β – γ = α + δ,  то есть ∠BDC= ∠BDA+ ∠CDA.  Это противоречит тому, что в любом трёхгранном угле сумма двух плоских углов больше третьего.

Не существует.