Задача
Четырёхугольник ABCD – вписанный. На его диагоналях AC и BD отметили точки K и L соответственно так, что AK = AB и DL = DC.
Докажите, что прямые KL и AD параллельны.
Решение
Решение 1:Поскольку четырёхугольник ABCD – вписанный, то ∠BAC = ∠BDC. Значит, в равнобедренных треугольниках ABK и DLC равны и углы при основаниях (см. рис.), следовательно, ∠BLC = ∠BKC, то есть четырёхугольник BCKL – вписанный. Таким образом, ∠KLO = ∠BCO = ∠BDA, то есть KL || AD.
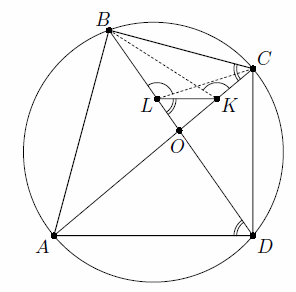
Решение 2:Из условия и подобия треугольников AOB и DOC получим, что AO : DO = AB : DC = AK : DL, откуда AK : AO = DL : DO. Следовательно,
OK : AO = OL : DO, значит, треугольники AOD и KOL подобны. Поэтому ∠KLO = ∠ADO, то есть KL || AD.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь