Задача
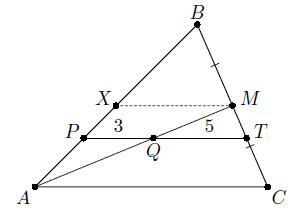
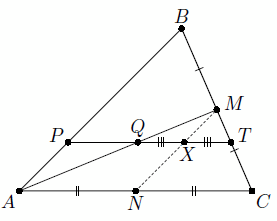
Дан треугольник ABC. Прямая, параллельная AC, пересекает стороны AB и BC в точках P и T соответственно, а медиану AM – в точке Q. Известно, что PQ = 3, а QT = 5. Найдите длину AC.
Решение
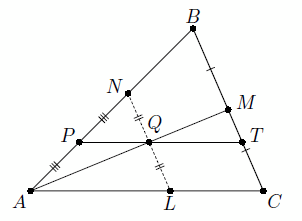
Первый способ. Проведём через точку Q прямую, параллельную BC (N и L – точки пересечения этой прямой со сторонами AB и AC соответственно, см. рис. слева). Поскольку AM – медиана, то LQ = NQ, кроме того, PT || AC, то есть PQ – средняя линия треугольника ANL. Значит, AL = 2PQ = 6. Кроме того, QL || TC и QT || LC, следовательно, LQTC – параллелограмм, откуда LC = QT = 5. Таким образом,
AC = AL + LC = 6 + 5 = 11.
Ответ
AC = 11.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет