Задача
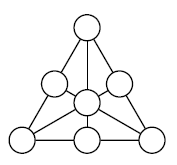
Можно ли в кружках (см. рисунок) разместить различные натуральные числа таким образом, чтобы суммы трёх чисел вдоль каждого отрезка оказались равными?
Решение
Пусть требуемая расстановка существует, S – сумма всех расставленных чисел, a и b – числа, стоящие в кружках, расположенных в каких-либо двух вершинах треугольника. Тогда для той вершины, в которой стоит число a, сумма чисел вдоль трёх отрезков, содержащих эту вершину, равна S + 2a. Аналогично для вершины, в которой стоит число b, эта сумма равна S + 2b. Так как суммы чисел вдоль каждого отрезка равны, то S + 2a = S + 2b, то есть a = b. Но это противоречит условию.
Ответ
Нельзя.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет