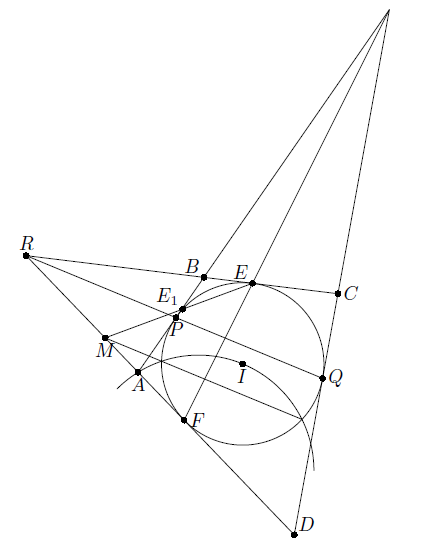
Рассмотрим точку R пересечения BC и AD и центр I окружности ω. Прямая IR пересекает отрезок EF в его середине R'. При этом R' – образ точки R при инверсии относительно ω (см. задачу 158326). Опустим перпендикуляр RS' на IS. Так как прямая EF проходит через S, то прямоугольные треугольники IRS' и ISR' подобны. Следовательно, S' – образ точки S при инверсии относительно ω, то есть R лежит на одной прямой с двумя другими точками касания P и Q окружности со сторонами четырёхугольника.

  Пусть прямая EE₁ пересекает AD в точке M. Рассмотрим три окружности: ω, Ω и описанную окружность Ω₃ треугольника AID. Заметим, что радикальная ось Ω₃ и ω является средней линией треугольника FPQ. Действительно, рассмотрим середины U, V отрезков FP, AI и центр O окружности Ω₃. Степень точки U относительно ω равна  UI² – FI² = – UF²  и относительно Ω₃ такая же:

UO² – AO² = UV² + VO² – AO² = UV² – AV² = UV² – FV² = – UF²,   то есть U лежит на радикальной оси. То же верно для середины отрезка FQ.

  Так как две другие радикальные оси пересекаются в точке M,  RM = MF (см. рис.).

  Аналогично FF₁ пересекает BC в середине N отрезка RE. Следовательно, прямые EE₁ и FF₁ симметричны относительно биссектрисы угла ERF. Значит, точки E₁ и F₁ также симметричны и EFF₁E₁ – равнобокая трапеция.

Ответ задачи отсутствует