Задача
В треугольнике ABC ALa и AMa – внутренняя и внешняя биссектрисы угла A. Пусть ωa – окружность, симметричная описанной окружности Ωa треугольника ALaMa относительно середины BC. Окружность ωb определена аналогично. Докажите, что ωa и ωb касаются тогда и только тогда, когда треугольник ABC прямоугольный.
Решение
Решение 1: Известно, что окружность Ωa перпендикулярна описанной окружности Ω треугольника ABC и является геометрическим местом точек X, для которых BX : CX = BA : CA (окружность Аполлония, см. задачу 157142). Окружность ωa симметрична Ωa относительно серединного перпендикуляра к BC и потому также перпендикулярна Ω и является геометрическим местом точек X, для которых BX : CX = CA:BA. Аналогичный факт верен и для ωb. Значит, множество общих точек ωa и ωb переходит в себя при инверсии относительно Ω. Поэтому они касаются тогда и только тогда, когда некоторая их общая точка X лежит на Ω; при этом AX : BX : CX = BC : CA : AB.
Итак, если окружности касаются, то по теореме Птолемея (см задачу 152468) одно из произведений AX·BC, BX·CA, CX·AB равно сумме двух других. Так как эти произведения пропорциональны квадратам сторон треугольника ABC, он должен быть прямоугольным.
Наоборот, пусть треугольник ABC прямоугольный, и точки A, B, C, X (в некотором порядке) образуют прямоугольник. Тогда эти точки лежат на одной окружности, и нетрудно убедиться, что AX : BX : CX = BC : CA : AB; это значит, что X – общая точка ωa и ωb, а это равносильно тому, что они касаются.
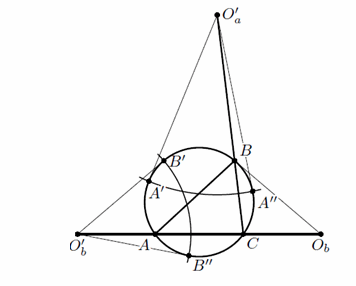
Решение 2: Центр Oa окружности Ωa лежит на касательной к Ω в точке A. Кроме того, известно, что точки Oa, Ob, Oc лежат на одной прямой. Центр O'a окружности ωa симметричен Oa относительно середины BC, а её радиус равен длине касательной O'aA', проведённой из O'a к Ω (точка A' симметрична A относительно серединного перпендикуляра к BC).
Точка X пересечения двух из окружностей ωa, ωb, ωc удовлетворяет соотношениям AX : BX : CX = BC : CA : AB, то есть лежит и на третьей окружности. Значит, если две из окружностей ωa, ωb, ωc касаются в точке X, то третья также проходит через эту точку и касается их обеих (ибо больше не имеет с ними общих точек).
Это замечание позволяет ограничиться случаем, когда C – наибольший угол треугольника ABC. Если ∠C = 90° (см. рис.), то касательные из точек O'a и O'b к Ω касаются её в одной и той же точке A' = B', диаметрально противоположной C. Значит, точки O'a, O'b, A' лежат на одной прямой и, следовательно, окружности с центрами O'a, O'b, проходящие через A', касаются в ней.
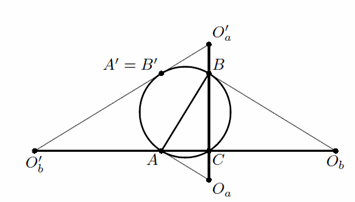
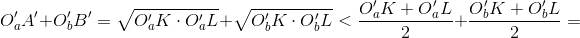
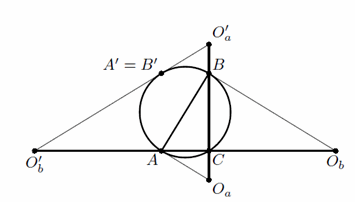 значит, сумма радиусов меньше расстояния между центрами, и окружности не имеют общих точек.
значит, сумма радиусов меньше расстояния между центрами, и окружности не имеют общих точек.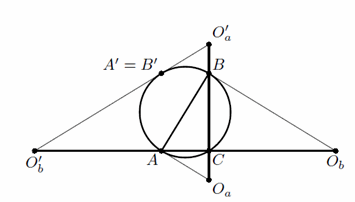
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь