б) См. рисунок к задаче 198192.   в) Для квадрата n×n клеток аналогично можно составить многосвязную компоненту, разбитую на прямоугольники d×2d, где d – длина диагонали клетки (сторона клетки считается равной 1), так, что непокрытая ею площадь квадрата – бордюр – будет составлена из равнобедренных прямоугольных треугольников с гипотенузами 4 или с катетами 4, 3 или 2, лежащими на сторонах квадрата (см. рис.).

  В прямоугольнике d×2d площади 4 и треугольнике с гипотенузой 4 и той же площади размещается по одной компоненте; в угловых треугольниках площади  S = 8  – 3 компоненты, площади  S = 4,5  – 2 компоненты, площади  S = 2  – одна компонента. Так как отношение S к числу компонент для каждого случая меньше 4, то (даже если не считать "многосвязную" компоненту) общее число компонент не меньше четверти площади квадрата, то есть не меньше ^n²/₄.

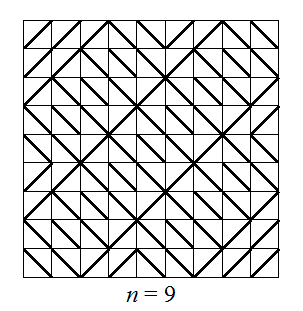
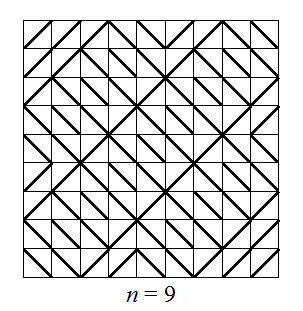
Ответ задачи отсутствует