Решение 1:   Пусть продолжение перпендикуляра, опущенного на прямую BD из точки M, пересекает сторону AD в точке E (см. рис.). Мы хотим доказать, что прямые CE и BM перпендикулярны.

  Обозначим через F точку пересечения прямых ME и BC и посмотрим на треугольник BDF: в нём высоты DC и FE пересекаются в точке M. Значит, и прямая BM является высотой этого треугольника,  BM ⊥ DF.

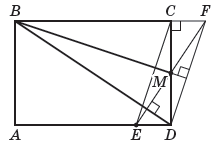
  Но четырёхугольник CFDE является параллелограммом (треугольники EMD и FMC равны по катету и острому углу, поэтому отрезки CF и ED равны и параллельны). Следовательно, прямая BM, перпендикулярная DF, перпендикулярна и CE.

Решение 2:   Пусть  BC = a,  CM = MD = b,  перпендикуляр, опущенный из C на BM, пересекает AD в точке E₁, а перпендикуляр, опущенный из M на BD, пересекает AD в точке E₂ (см. рис.).

  Из равенства углов E₁CD и MBC следует подобие треугольников E₁CD и MBC, откуда  E₁D = ^2b²/_a.  Аналогично из подобия треугольников E₂MD и DBC следует, что  E₂D = ^2b²/_a.  Итак,  E₁D = E₂D,  то есть точки E₁ и E₂ совпадают.

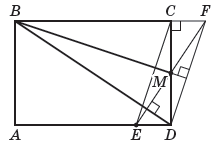
Ответ задачи отсутствует