Решение 1:Прямые AE и BF перпендикулярны, поскольку получаются друг из друга поворотом на 90° вокруг центра квадрата. Пусть прямая, проходящая через A и параллельная BF, пересекает прямую CD в точке G. Так как ABFG – параллелограмм, то  FG = AB  и, значит,  FD = DG.  По теореме Фалеса прямая, проходящая через D и параллельная BF, является медианой треугольника ADP. Поскольку  AE ⊥ BF,  эта прямая является и высотой. Следовательно, треугольник ADP – равнобедренный, как и треугольник AED. Угол EAD в обоих треугольниках является углом при основании, поэтому углы при вершинах также равны.

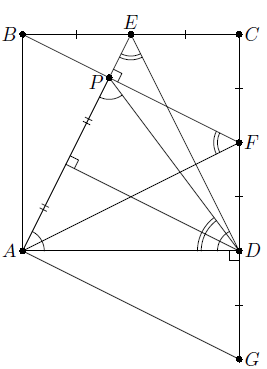
Решение 2:∠APF = 90° = ∠ADF. Значит, четырёхугольник APFD вписан, откуда  ∠ADP = ∠AFP = ∠AFB.  С другой стороны,  ∠AFB = ∠AED,  поскольку треугольники ABF и ADE равны.

Решение 3:Пусть  AB = 1.  Поскольку BP – высота прямоугольного треугольника с катетами 1 и ½, то  AP : PE = 4 : 1.  По теореме Фалеса проекция отрезка DP на CD равна ⁴/₅. Аналогично получаем, что его проекция на AD равна ³/₅. Значит, по теореме Пифагора  DP = 1 = AD.  Дальнейшие рассуждения такие же, как в решении 1.

Ответ задачи отсутствует