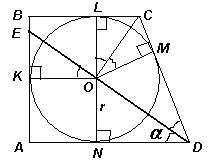
Пусть ABCD – данная трапеция c меньшей боковой стороной АВ, тогда биссектриса её острого угла D проходит через центр О окружности, вписанной в трапецию, и пересекает сторону АВ в точке Е (см. рис.). Заметим, что сумма углов OCD и ODC равна 90°, то есть  CO ⊥ DO.  Обозначим точки касания вписанной окружности со сторонамиАВ, ВС, CDиDAчерезK, L, MиNсоответственно (см. рис.). Поскольку ∠KOE= ∠ADE< 45°  иBKOL– квадрат, точкаЕлежит на отрезкеBK. Далее можно рассуждать по-разному.  Первый способ. ТрегольникиONDиOMDравны по катету и гипотенузе; аналогично, равны треугольникиOLCиOMC. Кроме того, треугольникиOKEиOLCравны по катету и острому углу.   Таким образом,  S_ADE = S_OND + S_AKON + S_OKE = S_OMD + S_BKOL + S_OMC = S_OMD + S_BEOL + S_OLC + S_OMC = S_CDEB,  то есть биссектрисаDEделит площадь трапеции пополам.

  Второй способ. Пусть биссектриса угла BCD пересекает прямую AD в точке F (см. рис.). DO – высота треугольника CDF, значит, этот треугольник – равнобедренный:  FD = CD.  Так как  AD > CD,  то точка F лежит на стороне AD.

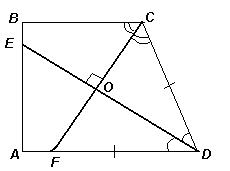
  Рассмотрим поворот с центром О на 90° по часовой стрелке. Так как AKON и BKOL – равные квадраты, то образом точки А при таком повороте является точка В. Образом луча OF является луч ОЕ, а образом прямой DA – прямая АВ, поэтому точка F при этом повороте переходит в точку Е. Кроме того, образом прямой АВ является прямая ВС, поэтому точка Е переходит в точку С. Таким образом, четырёхугольник ОЕВС является образом четырёхугольника OFAE, следовательно, эти четырёхугольники равны.  Так как треугольникиCODиFODтоже равны, то биссектрисаDEделит площадь трапеции пополам.

1 : 1.