Решение 1:   MN – диаметр описанной окружности треугольника СMN (см. рис). Пусть эта окружность пересекает диагональ АС в точке О.

  Так как СО – биссектриса угла MCN, то  OM = ON. Так как  ∠MAN = ½ ∠MОN,  то окружность с центром О, которая проходит через точки M и N, содержит также и точку А, то есть является описанной окружностью треугольника AMN.

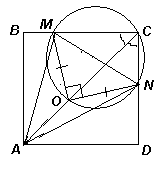
Решение 2:   Так как точка А лежит на биссектрисе угла С треугольника MCN и  ∠MAN = 90° – ½ ∠MСN,  то А – центр вневписанной окружности треугольника MCN (см. задачу 155448). Пусть I – центр вписанной окружности треугольника MCN (см. рис.), тогда  ∠AMI = ∠ANI = 90°,  значит, точки M и N лежат на окружности с диаметром AI. Следовательно, центр О описанной окружности треугольника AMN лежит на АС.

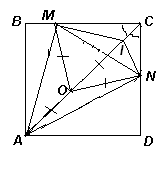
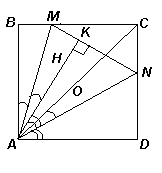
Решение 3:   Отразим вершины В и D относительно прямых АМ и АN соответственно (см. рис.). Так как  ∠MAB + ∠NAD = 45° = ∠MAN,  то их образы B' и D' лежат на одном луче с началом в точке А. Кроме того,  ∠АВ'M = ∠АВC = 90°  и  ∠АD'N = ∠АDC = 90°,  поэтому точки B' и D' лежат на отрезке MN. Таким образом, B' и D' – это одна и та же точка K, которая является основанием высоты треугольника MAN.

  Согласно задаче 152358  ∠KAM = ∠OAN.  Значит,  ∠OAD = ∠OAN + ∠NAD = ∠KAM + ∠NAD = ∠MAB + ∠NAD = 45°,  то есть точка О лежит на АС.

Ответ задачи отсутствует