Задача
Можно ли n раз рассадить 2n + 1 человек за круглым столом, чтобы никакие двое не сидели рядом более одного раза, если
а) n = 5; б) n = 4; в) n – произвольное натуральное число?
Решение
Задачу эквивалентна следующей:
можно ли в полном графе с 2n + 1 вершиной провести n гамильтоновых циклов, не имеющих общих рёбер?
Действительно, обход такого цикла задает порядок рассадки за круглым столом – в порядке обхода вершин. В цикл входит 2n + 1 ребро, а всего рёбер n(2n + 1), поэтому при положительном ответе все рёбра будут задействованы в циклах по одному разу. а) На рисунке показано, как разбить на три цикла рёбра полного 7-вершинного графа: каждый цикл содержит все диагонали (или стороны) фиксированной длины правильного семиугольника.
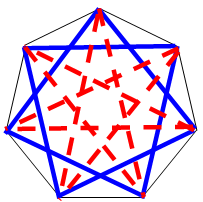
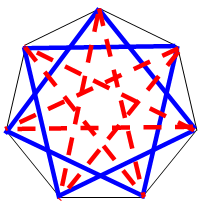
Ответ
Можно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь