Задача
На плоскости нарисованы два выпуклых многоугольника P и Q. Для каждой стороны многоугольника P многоугольник Q можно зажать между двумя прямыми, параллельными этой стороне. Обозначим через h расстояние между этими прямыми, а через l – длину стороны и вычислим произведение lh. Просуммировав такие произведения по всем сторонам P, получим некоторую величину (P, Q). Докажите, что (P, Q) = (Q, P).
Решение
Пусть ai , bj – векторы сторон многоугольников P и Q соответственно. Расстояние hi, вычисленное, как указано в условии, для стороны ai многоугольника P, равно, очевидно, длине проекции Q на прямую, перпендикулярную ai, то есть половине суммы проекций сторон bj на эту прямую. Умножив на
li = |ai|, получим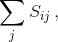 
где Sij – площадь параллелограмма Пij, построенного на векторах ai и bj. Поэтому 
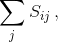Вычисляя
(Q, P), мы получим тот же результат (с заменой порядка суммирования).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь