Задачи и олимпиады по математике

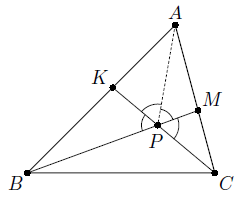
Задача

На стороне AB треугольника ABC отмечена точка K, а на стороне AC – точка M. Отрезки BM и CK пересекаются в точке P. Оказалось, что углы APB, BPC и CPA равны по 120°, а площадь четырёхугольника AKPM равна площади треугольника BPC. Найдите угол BAC.

Решение

К обеим частям равенства S_AKPM = S_BPC прибавим площадь треугольника BPK (см. рис.). Получим, что S_ABM = S_BCK. Следовательно,

^AM/_AC·S_ABC = ^BK/_AB·S_ABC , то есть BK : AB = AM : AC. Таким образом, точки K и M делят отрезки BA и AC в одном и том же отношении, считая от вершин B и A соответственно, то есть BK : KA = AM : MC. (*)

Заметим теперь, что ∠BPK= ∠KPA= ∠APM= ∠MPC= 60°. Значит,PKиPM– биссектрисы треугольниковAPBиAPCсоответственно. По свойству биссектрисы треугольника BK:KA = BP:PA и AM:MC = AP:PC. Учитывая равенство (*), получим BP:PA = AP:PC. Таким образом, треугольникиBPAиAPCподобны (по двум сторонам и углу между ними). Следовательно, ∠PAC= ∠PBA. Значит, ∠BAC= ∠BAP+ ∠PAC= ∠BAP+ ∠PBA= 180° – 120° = 60°.

Ответ

60°.

Задача

Решение

Ответ

Подтверждение удаления