Нам потребуются два почти очевидных утверждения.   1. Если четырёхугольник вписан, то точка в пространстве, равноудалённая от трёх его вершин, равноудалена и от всех четырёх.   2. Пусть отрезок, соединяющий точки на боковых сторонах трапеции (или параллелограмма), делит её на два четырёхугольника. Если один из них вписанный, то и второй вписанный.

  (Действительно, из условия следует, что соответствующие углы этих четырёхугольников равны.)   Для решения задачи достаточно доказать, что шестигранник, соседний с вписанным, является вписанным.

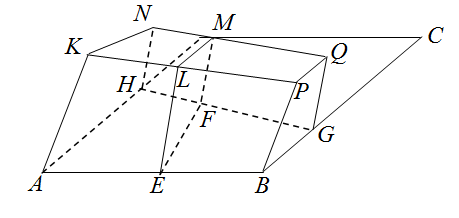
  Пусть ABCD – нижняя грань параллелепипеда, AEFHKLMN и EBGFLPQM – соседние шестигранники (см. рисунок), первый из которых вписанный. Тогда все его грани – вписанные четырёхугольники.

  Рассмотрим центр O описанной сферы тетраэдра BEGP. Он равноудален от точек B, E, G, P. Четырёхугольники BEFG и BELP вписанные (поскольку ABGH и ABPK – трапеции), значит, к этому набору равноудалённых от O точек добавляются F и L. Теперь к этому набору можно добавить точку M (четырёхугольник EFML вписан) и наконец точку Q (четырёхугольник PQML вписан, поскольку KPQN – трапеция). Итак, O равноудалена от всех вершин шестигранника EBGFLPQM, то есть является центром описанной вокруг него сферы.

Ответ задачи отсутствует