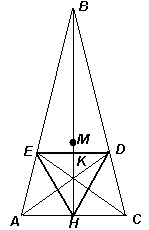
Приведём один из возможных контрпримеров. Рассмотрим равнобедренный треугольник АВС, в котором  АВ =ВС = 3,  АС = 1  (см. рис.). Пусть ВН – его высота, АD и CE – биссектрисы, M – точка пересечения медиан. Тогда  BE : EA = BD : DC = AB : AC = 3 : 1.

Пусть отрезок DE пересекает ВН в точке K, тогда BK : KH = 3 : 1  (по теореме о пропорциональных отрезках). А  BM : MH = 2 : 1.  Следовательно, точка G лежит вне треугольника DEH, образованного основаниями биссектрис.

Неверно.