Задача
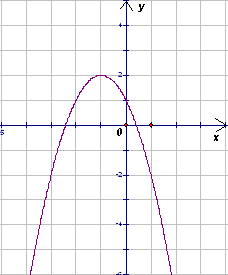
На координатной плоскости изображен график функции y = ax² + bx + c (см. рисунок).
На этой же координатной плоскости схематически изобразите график функции y = cx² + 2bx + a.

Решение
Вычислим значения a, b и c. Первый способ. На графике лежат точки (0, 1), (1, –2) и (–1, 2). Значит, c = y(0) = 1, a + b + c = y(1) = –2, a + b – c = y(–1) = 2. Отсюда a = –1,
b = –2, c = 1. Второй способ. Данный график получается параллельным переносом графика функции y = – x², поэтому a = –1. Значение b = –2 вычисляется из равенства – b/2a = –1 (абсцисса вершины параболы), а с = y(0) = 1. Следовательно, искомый график задается уравнением y = x² – 4x – 1 = (x – 2)² – 5.
Ответ
Cм. рисунок.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь