Задача
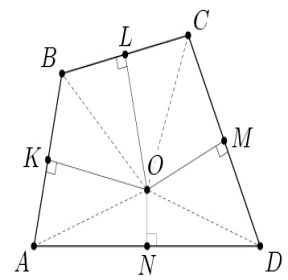
Дан четырёхугольник АВСD площади 1. Из его внутренней точки О опущены перпендикуляры OK, OL, OM и ON на стороны АВ, ВС, CD и DA соответственно. Известно, что AK ≥ KB, BL ≥ LC, CM ≥ MD и DN ≥ NA. Найдите площадь четырёхугольника KLMN.
Решение
Из двух наклонных, проведённых из одной точки больше та, у которой проекция больше. Поэтому из неравенств, заданных в условии задачи, следует, что ОА ≥ OB ≥ OC ≥ OD ≥ OA. Значит, ОА = OB = OC = OD, то есть О – центр окружности, описанной около четырёхугольника АВСD (см. рис.). Поэтому точки K, L, M и N являются серединами сторон АВСD. Следовательно, согласно задаче 156493 а) SKLMN = ½ SABCD = ½.
Ответ
0,5.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет