Задача
Положительные числа a, b, c и d удовлетворяют условию 2(a + b + c + d) ≥ abcd. Докажите, что a² + b² + c² + d² ≥ abcd.
Решение
Возможны два случая.
1) abcd ≥ 16. Тогда по неравенству между средними квадратичным и арифметическим a² + b² + c² + d² ≥ 4(a+b+c+d/4)² ≥ 4(abcd/8)² = 1/16 (abcd)² ≥ abcd. 2) abcd < 16. Тогда 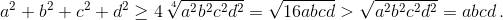
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет