Задача
Обозначим через d(n) количество разбиений числа n на различные слагаемые, а через l(n) – на нечётные. Докажите равенства: а) d(0) + d(1)x + d(2)x² + ... = (1 + x)(1 + x²)(1 + x³)...; б) l(0) + l(1)x + l(2)x² + ... = (1 – x)–1(1 – x³)–1(1 – x5)–1...; в) d(n) = l(n) (n = 0, 1, 2, ...).(Считается по определению, что d(0) = l(0) = 1.)
Решение
а) В соответствии, описанном в решении задачи 161509, чтобы получить одночлен, соответствующий разбиению на различные слагаемые, нужно из каждой скобки брать либо единицу, либо член наименьшей степени. Это и значит, что от каждой скобки останутся только два первых члена. В результате мы и получим правую часть равенства а). б) В том же соответствии, чтобы получить одночлен, соответствующий разбиению на нечётные слагаемые, нужно из чётных скобок брать только единицу – фактически в произведении останутся только нечётные скобки, то есть правая часть равенства б). в) Первый способ.
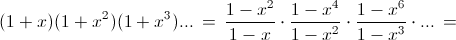
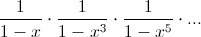
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь