Задача
При возведении числа 1 + 
в различные степени, можно обнаружить некоторые закономерности:
(1 + )1 = 1 + = + 
, (1 + )2 = 3 + 2 = 
+ 
, (1 + )3 = 7 + 5 = 
+ 
, (1 + )4 = 17 + 12 = 
+ 
.
Для их изучения определим числа an и bn при помощи равенства (1 + )n = an + bn, (n ≥ 0).
а) Выразите через an и bn число (1 – )n.
б) Докажите равенство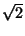 
в) Каким рекуррентным уравнениям удовлетворяют последовательности {an} и {bn}?
г) Пользуясь пунктом а), найдите формулы n-го члена для последовательностей {an} и {bn}.
д) Найдите связь между числами an, bn и подходящими дробями к числу .
Решение
б)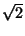
в) Из равенства (an + bn)(1 + ) = (an+1 + bn+1) находим, что числа an и bn удовлетворяют рекуррентным соотношениям an+1 = an + 2bn,
bn+1 = an + bn. Отсюда an+2 = 2an+1 + an = 0, bn+2 = 2bn+1 + bn = 0 (n ≥ 0).
д) См. задачу 160618.
Ответ
а) (1 – )n = an – bn; в) an+2 = 2an+1 + an, bn+2 = 2bn+1 + bn;
г) an = ½ ((1 + )n + (1 – )n),
bn = 
((1 + )n – (1 – )n); д) Pn/Qn = an+1/bn+1.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь