Задача
Докажите неравенства:
а)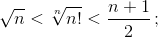 
б) 
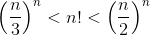при n > 1; в) 
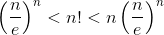при n > 6.
Решение
а) Левое неравенство доказано в задаче 178152. Правое неравенство следует из неравенства Коши. б) Заметим, что n! > 2n–1. Следовательно,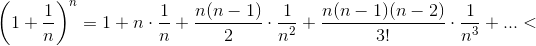 
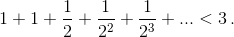
Докажем левое неравенство по индукции. База (n = 1) очевидна.
Шаг индукции.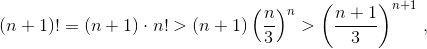 
поскольку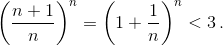 
Правое неравенство доказывается аналогично с использованием очевидного неравенства (1 + 1/n)n > 2 при n > 1. в) Заметим, что последовательность (1 + 1/n)n возрастает. Действительно,
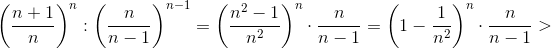
(мы использовали неравенство Бернулли, см. задачу 130899).
С другой стороны, последовательность (1 + 1/n+1) убывает. Действительно,
Поскольку число e по определению равно 
то 
Докажем оба неравенства по индукции. База (n = 7) проверяется непосредственно.
Шаг индукции. 
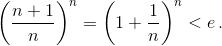
поскольку 
поскольку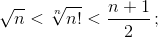 
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь